Penerapan konsep program linear

Penerapan Konsep Program Linear Dalam Kehidupan Sehari-Hari

Penerapan Konsep Program Linear Dalam Kehidupan Sehari-Hari

A. Pengertian Program linear
Program Linear adalah suatu cara untuk penyelesaian masalah dengan menggunakan persamaan atau pertidaksamaan linear yang
mempunyai banyak penyelesaian, dengan memperhatikan syarat-syarat agar diperoleh hasil yang maksimum/minimum (penyelesaian optimum).
Program linear merupakan suatu model umum yang dapat digunakan dalam pemecahan pengalokasian sumber-sumber yang terbatas secara optimal. Masalah tersebut timbul apabila
seseorang diharuskan untuk memilih atau menentukan tingkat setiap kegiatan yang akan dilakukan, dimana masing-masing kegiatan membutuhkan sumber yang sama sedangkan jumlahnya terbatas.
Program linear berasal dari kata
pemrograman dan linear. Pemrograman artinya perencanaan dan linear berarti bahwa fungsi-fungsi yang digunakan merupakan fungsi linear.
Jadi, program linear adalah suatu teknik perencanaan yang bersifat analitis yang analisisnya memakai model matematika, dengan tujuan menemukan beberapa kombinasi alternatif pemecahan masalah.
Kemudian dipilih yang terbaik diantaranya dalam rangka menyusun langkah-langkah kebijaksanaan lebih lanjut tentang alokasi sumber daya dan dana yang terbatas. Kegunaannya adalah mencapai tujuan dan sasaran yang diinginkan secara optimal.
Penerapan konsep Program Linear dalam kehidupan sehari-hari:
● Program linear merupakan salah satu teknik penelitian operasional yang digunakan paling luas dan diketahui dengan baik, serta berupa metode matematik, yang berfungsi mengalokasikan sumber daya yang langka untuk mencapai tujuan tunggal seperti memaksimumkan keuntungan dan meminimumkan biaya. Program linear banyak diterapkan dalam membantu menyelesaikan masalah ekonomi, industri, militer, dan sosial.
Program linier berkaitan dengan penjelasan suatu dunia nyata sebagai suatu model matematik yang terdiri atas sebuah fungsi tujuan dan sistem kendala linier.
● Program linear digunakan untuk memecahkan masalah pengoptimalan (memaksimalkan atau meminimalkan suatu tujuan). Dari sini program linear dapat digunakan untuk menyelesaikan
masalah-masalah manusia. Dalam kehidupan sehari-hari tentu banyak masalah yang berkaitan dengan perhitungan, seperti dalam berdagang. Dalam berdagang seorang pedagang pasti ingin mendapat keuntungan atau laba yang besar/maksimum, maka program linear dapat digunakan untuk menghitung maksimum laba yang bisa diperoleh seorang pedagang.
Suatu masalah dikatakan masalah program linier jika :
1. Terdapat tujuan yang dicapai, dan dalam model matematika fungsi tujuan ini dalam bentuk linier.
2. Terdapat sumber daya atau masukan (input) yang berada dalam keadaan terbatas, dapat dirumuskan dalam hubungan yang linear yaitu pertidaksamaan linear.
3. Pola umum masalah yang dapat dimodelkan dengan program linier harus memenuhi:
a. Adanya pilihan kombinasi beberapa faktor kegiatan,
b. Adanya sumber penunjang beserta batasnya,
c. Adanya fungsi obyektif/sasaran/tujuan yang harus dioptimumkan,
d. Bahwa relasi yang timbul antara faktor-faktor semuanya linier.
B. Contoh Soal:
Soal 1
1. Tanah seluas 10.000 m² akan dibangun rumah tipe A dan tipe B. Untuk rumah tipe A diperlukan 100 m² dan tipe B diperlukan 75 m². Jumlah rumah yang dibangun paling banyak 125 unit. Keuntungan rumah tipe A adalah Rp 6.000.000,00/unit dan tipe B adalah Rp 4.000.000,00/unit. Keuntungan maksimum yang dapat diperoleh dari penjualan rumah tersebut adalah ……..
A . Rp 550.000.000,00
B . Rp 600.000.000,00
C . Rp 700.000.000,00
D . Rp 800.000.000,00
E . Rp 900.000.000,00
Jawab:
Misalnya:
x = rumah tipe A
y = rumah tipe B
100x + 75y ≤ 10.000 dibagi 25 ⇒
4x + 3y ≤ 400 …..(1)
x + y ≤ 125 …..(2)
Keuntungan maksimum : 6000.000 x + 4000.000 y =…?
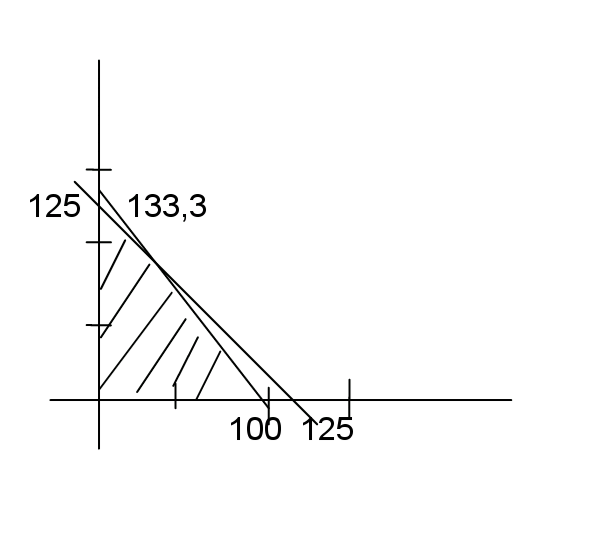
Mencari keuntungan maksimum dengan mencari titik-titik pojok dengan menggunakan sketsa grafik:


Titik potongnya (0 , 125)
Gambar grafiknya:

Persamaan kuadrat

Persamaan Kuadrat

Persamaan kuadrat itu adalah persamaan yang memiliki variabel yang berpangkat dua. Biasanya yang berpangkat dua itu adalah x. Sehingga bentuk umum persamaan kuadrat adalah:

ax² + bx +c =0

dengan syarat: a tidak sama dengan nol, dan a, b, dan c adalah elemen himpunan bilangan Real.

Kenapa disebut persamaan, karena ada tanda sama dengan '=' itu. Jadi kalau tandanya tidak '=' seperti tanda 'kurang dari' < atau 'lebih dari' >, itu akan disebut sebagai pertidaksamaan.

Persamaan kuadrat itu memiliki penyelesaian yaitu akar-akar dari persamaan kuadrat, yang biasanya ada dua yaitu x₁ dan x₂. Disebut penyelesaian karena jika nilai dari salah satu penyelesaian itu dimasukkan pada variabel x pada persamaan akan menghasilkan nilai nol. Sehingga akar-akar persamaan kuadrat juga disebut faktor pembuat nol.

Adapun cara untuk mencari akar-akar persamaan kuadrat ada tiga, yaitu :

1. Memfaktorkan
• cara I
• cara II
• cara III
2. Melengkapkan Kuadrat Sempurna
3. Menggunakan Rumus ABC

Yang kalau diringkas bisa disebut 3M. Wah seperti memberantas sarang nyamuk saja, hehe. Yuk sekarang coba kita bahas satu persatu.

• Memfaktorkan

Cara yang pertama ini paling tepat digunakan jika nilai a pada variabel x² dari persamaan ax² + bx + c = 0 adalah 1 (satu). Atau secara lebih mudah yaitu x² didepannya tidak mengandung angka lain selain variabel x itu sendiri. Contoh persamaan kuadratnya :

1. x² - 8x + 15 = 0
2. x² - x - 12 = 0
3. x² + 8x + 12 = 0
4. x² - 8x + 16 = 0
5. x² - 9 = 0

Adapun langkah-langkah untuk mencari akar-akar persamaan kuadratnya adalah sebagai berikut, dimana contoh yang kita pakai adalah persamaan kuadrat yang no. 1 yakni x² - 8x + 15 = 0. (langkah 1) : Tulis persamaan kuadrat itu, seperti berikut ini : x² - 8x + 15 = 0 (langkah 2) : Tulis dibawahnya dua buah tanda kurung, dengan masing-masing diisi variabel x seperti berikut : (x )(x ) = 0 (langkah 3) : Pikirkan dua buah angka, yang jika dikalikan hasilnya adalah 15, dan jika dua angka itu dijumlahkan hasilnya -8 (negatif 8). Maka tentunya kita akan memikirkan 1 dan 15, atau 3 dan 5, karena hanya dua pasangan bilangan itu yang jika dikalikan menghasilkan 15. Terus agar hasil kalinya positif 15 dan hasil penjumlahan -8, maka yang paling tepat adalah -3 dan -5. Coba kita jumlahkan -3 dan -5 yaitu -3 + (-5) = -8. Betulkan hasilnya -8. Kalau sampai disini masih bingung, kenapa jika dikali hasilnya harus 15? Lihat kembali persamaan kuadratnya yaitu x² - 8x + 15 = 0. Jadi jika dikali harus menghasilkan c yaitu 15, dan jika dijumlah harus menghasilkan koefisien x, yaitu b. Yang mana b, yang mana c? Kita lihat lagi bentuk umum persamaan kuadrat yaitu ax² + bx + c = 0. Jadi c adalah bilangan konstanta-nya (yang tidak berisi variabel x), dan b adalah koefisien dari variabel x yang berpangkat satu(x tanpa pangkat), dan koefisien dari variabel x yang berpangkat 2 atau x² adalah a, dalam hal ini nilai a = 1. Jadi angka 1 tidak usah ditulis ya didepan x² seperti aturan yang sudah biasa. (langkah 4) : Masukkan kedua angka itu ke dalam masing-masing tanda kurung, lengkap dengan tanda negatif atau positifnya, seperti berikut ini : (x - 3)(x - 5) = 0 (langkah 5) : Samakan masing-masing setiap suku dalam tanda kurung dengan 0 (nol), seperti berikut ini : (x - 3) = 0 x - 3 = 0 x = 3 (tanda negatif pada 3 hilang karena pindah ruas) Sebenarnya ada teori mendasar mengenai kenapa kalau pindah ruas bisa berubah tanda, dan itu akan saya jelaskan pada posting khusus, agar kita bisa lebih konsentrasi pada materi ini. Jadi kita dapatkan nilai x₁ = 3. Selanjutkan kita samakan lagi suku yang lagi satu dengan nol, yaitu : (x - 5) = 0 x - 5 = 0 x = 5 Jadi kita dapatkan x₂ = 5. Jadi adapun akar-akar persamaan kuadrat x² - 8x + 15 = 0 adalah x₁ = 3 dan x₂ = 5, atau bisa juga disebut sebagai himpunan penyelesaian dari persamaan kuadrat x² - 8x + 15 = 0 adalah HP = {3, 5}. Nah, gampang sekali bukan untuk memahami cara yang pertama. Selanjutnya untuk lebih memantapkan bisa dicoba contoh persamaan kuadrat di atas yang nomor 2 sampai nomor 5.

•  Memakai Rumus Kuadrat atau Rumus abc

 

dimana b² – 4ac disebut dengan Diskriminan ( D ). jadi D = b² – 4ac. Rumus inilah yang kita gunakan dalam menentukan akar-akar persamaan kuadrat.

Contoh Soal :
Tentukan akar-akar dari persamaan kuadrat 2x² + 3x -9 = 0, ( a=2| b=3| c=-9 )!

• Melengkapkan Kuadrat Sempurna

 Bentuk umum persamaan kuadrat bebentuk kuadrat sempurna adalah :
dengan q > 0
Penyelesaian dengan cara ini cukup rumit jadi hati-hatilah dalam penyelesaiannya. Dengan metode ini kita akan mengubah bentuk ax² – bx – c = 0 menjadi (x + p)² = q sehingga penyelesaiannya x = -p ± √q . Langkah pertama, ubah menjadi bentuk kemudian menambahkan kedua ruas denganhal ini akan menjadikannya kuadrat sempurna.

Contoh Soal :
Tentukan himpunan penyelesaian dari x² + 13 = 6x

aritmatika sosial

ARITMATIKA SOSIAL

A. Harga pembelian, harga penjualan, untung, dan rugi
Dalam kehidupan sehari-hari sering kali kita menjumpai atau melakukan kegiatan jual beli atau perdagangan. Dalam perdagangan terdapat penjual dan pembeli. Jika kita ingin memperoleh barang yang kita inginkan maka kita harus melakukan pertukaran untuk mendapatkannya. Misalnya penjual menyerahkan barang kepada pembeli sebagai gantinya pembeli menyerahkan uang sebagai penganti barang kepada penjual.
Seorang pedagang membeli barang dari pabrik untuk dijual lagi dipasar. Harga barang dari pabrik disebut modal atau harga pembelian sedangkan harga dari hasil penjualan barang disebut harga penjualan.
Dalam perdagangan sering terjadi dua kemungkinan yaitu pedagan mendapat untung dan rugi.
1. Untung
Untuk memahami pengertian untung perhatikan contoh berikut:
Pak Umar membeli sebidang tanah dengan harga Rp 10.000.000,- kemudian karena ada suatu leperluan pak Umar menjual kembali sawah tersebut dengan harga Rp 11.500.000,-.
Ternyata harga penjualan lebih besar dibanding harga pembelian, berarti pak Umar mendapat untung.
Selisih harga penjualan dengan harga pembelian
=Rp 11.500.000,- – Rp 10.000.000,-
=Rp 1.500.000,-
Jadi pal Umar mendapatkan untung sebesar Rp 1.500.000,-
Berdasarkan contoh diatas, maka dapat ditarik kesimpulan:
Penjual dikatakan untung jika jika harga penjualan lebih besar dibanding dengan harga pembelian.
Untung = harga jual – harga beli
2. Rugi
Ruri membeli radio bekas dengan harga Rp 150.000,- radio itu diperbaiki dan menghabiskan biaya Rp 30.000,- kemudian Ruri menjual radio itu dan terjual dengan harga Rp 160.000,-
Modal (harga pembelian) = Rp 150.000,- + Rp 30.000,-
= Rp !80.000,-
Harga penjualan = Rp 160.000,-
Ternyata harga jual lebih rendah dari pada harga harga pembelian, jadi Ruri mengalami rugi.
Selisih harga pembelian dan harga penjualan:
=Rp 180.000,- – Rp 160.000,-
=RP 20.000,-
Berdasarkan uraian diatas penjual dikatakan rugi jika harga penjualan lebih rendah dibanding harga pembelian.
Rugi = harga beli – harga jual
3. Harga pembelian dan harga penjualan
Telah dikemukakan bahwa besar keuntungan atau kerugian dapat dihitung jika harga penjualan dan harga pembelian telah diketahui.
Besar keuntungan dirumuskan:
Untung =harga jual – harga beli
Maka dapat diturunkan dua rumus yaitu:
1. Harga jual = harga beli + Untung
2. Harga beli = harga jual – harga untung
Besar kerugian dirumuskan:
Rugi = harga beli – harga jual
Maka dapat diturunkan rumus:
1. Harga beli = harga jual + Rugi
2. Harga jual = harga beli – Rugi
B. Persentase untung dan rugi
1. Menentukan Persentase Untung atau Rugi
Pada persentase untung berarti untung dibanding dengan harga pembelian, dan persentase rugi berarti rugi dibanding harga pembelian.
Untung
Persentase Untung = X 100 %
Harga beli
Rugi
Persentase Rugi = X 100 %
Harga beli
Contoh:
a). Seorang bapak membeli sebuah mobil seharga Rp 50.000.000, karena sudah bosan dengan mobil tersebut maka mobil tersebut dijual dengan harga Rp 45.000.000,.Tentukan persentase kerugiannya!
Jawab:
Harga beli Rp 50.000.000
Harga jual Rp 45.000.000
Rugi = Rp 50.000.000 – Rp 45.000.000
= Rp 5.000.000
Rp 5.000.000
Rp 50.000.000
= Rp 10 %
Jadi besar persentase kerugiannya adalah 10 %.
b). Seorang pedagang membeli gula 5 kg dengan harga Rp 35.000, kemudian dijual dengan harga Rp 45.000, Berapakah besar persentase keuntungan pedagang tersebut?
Jawab:
Harga beli Rp 35.000,
Harga jual Rp 45.000,
Untung = Rp 45.000 – Rp 35.000
= Rp 10.000
Rp 10.000
Rp 35.000
= 28,7 %
Jadi persentase keuntungan adalah 28,7 %
2. Menentukan harga pembelian atau harga penjualan berdasarkan persentase untung atau rugi
Contoh:
Seorang pedagang membeli ikan seharga Rp 50.000 / ekor. Jika pedagang tersebut menghendaki untung 20 % berapa rupiahkah ikan tersebut harus dijual?
Jawab:
Harga beli Rp 50.000
Untung 20 % dari harga beli = = Rp 10.000
Harga jual = harga beli + untung
=Rp 50.000 +Rp 10.000
=Rp 60.000
Jadi pedagang itu harus menjual dengan harga Rp 60.000
Persentase untung atau rugi selalu dibandingkan terhadap harga pembelian (modal), kecuali ada keterangan lain.
Persentase Untung =
Persentase Rugi =
Hb = harga pembelian
C. Rabat(diskon), bruto, tara, dan neto
1. Rabat
    Rabat adalah potongan harga atau lebih dikenal dengan diskon.
Contoh:
Sebuah toko memberikan diskon 15 %, budi membeli sebuah rice cooker dengan harga Rp 420.000. berapakah harga yang harus dibayar budi?

Jawab:
Harga sebelum diskon = Rp 420.000
Potongan harga = 15 % x Rp 420.000 = Rp 63.000
Harga setelah diskon = Rp 420.000 – Rp 63.000 = Rp 375. 000
Jadi budi harus membayar Rp 375.000
Berdasarkan contoh diatas dapat diperoleh rumus:
Harga bersih = harga kotor – Rabat (diskon)
Harga kotor adalah harga sebelum didiskon
Harga bersih adalah harga setelah didiskon
2. Bruto, Tara, dan Neto
Dalam sebuah karung yang berisi pupuk tertera tulisan berat bersih 50 kg sedangkan berat kotor 0,08 kg, maka berat seluruhnya = 50kg + 0,08kg=50,8kg.
Berat karung dan pupuk yaitu 50,8 kg disebut bruto(berat kotor)
Berar karung 0,08 kg disebut disebut tara
Berat pupuk 50 kg disebut berat neto ( berat bersih)
Jadi hubungan bruto, tara, dan neto adalah:
 Neto = Bruto – T ara
Jika diketahui persen tara dan bruto maka untuk mencari tara digunakan rumus:
 Tara = Persaen Tara x Bruto
Untuk setiap pembelian yang mendapat potongan berat(tara) dapat dirumuskan:
 Harga bersih = neto x harga persatuan berat
D. Bunga tabungan dan pajak
1. Bunga tabungan (Bunga Tunggal)
Jika kita menyimpan uang dibank jumlah uang kita akan bertambah, hal itu terjadi karena kita mendapatkan bunga dari bank. Jenis bunga tabungan yang akan kita pelajari adalah bunga tunggal, artinya yang mendapat bunga hanya modalnya saja, sedangkan bunganya tidak akan berbunga lagi. Apabila bunganya turut berbunga maka jenis bunga tersebut disebut bunga majemuk.
Contoh:
Rio menabung dibank sebesar Rp 75.000 dengan bunga 12% per tahun. Hitung jumlah uang rio setelah enam bulan.
Jawab:
Besar modal (uang tabungan) = Rp 75.000
Bunga 1 tahun 12 % =
=
Bunga 6 bulan =
= Rp 4500
Jadi jumlah uang Rio setelah disimpan selama enam bulan menjadi:
= Rp 75.000 + Rp 4500
= Rp 79.500
Dari contoh tersebut dapat disimpulkan
Bunga 1 tahun = persen bunga x modal
Bunga n bulan = x persen bunga x modal
= x bunga 1 tahun
Persen bunga selalu dinyatakan untuk 1 tahun, kecuali jira ada ketersngan lain pada soal.
2. Pajak
Pajak adalah statu kewajiban dari masyarakat untuk menterahkan sebagian kekayaannya pada negara menurut peraturan yan di tetapkan oleh negara. Pegawai tetap maupun swasta negeri dikenakan pajak dari penghasilan kena pajak yang disebut pajak penghasilan (PPh). Sedangkan barang atau belanjaan dari pabrik, dealer, grosor, atau toko maka harga barangnya dikenakan pajak yang disebut pajak pertambahan nilai (PPN).
Contoh:
Seorang ibu mendapat gaji sebulan sebesar Rp 1.000.000 dengan penghasilan tidak kena pajak Rp 400.000. jira besar pajak penghasilan (PPh) adalah 10 % berapakah gaji yang diterima ibu tersebut?
Jawab:
Diketahui: Pesar penghasilan Rp 1.000.000
Penghasilan tidak kena pajak Rp 400.000
Pengahasilan kena pajak = Rp 1.000.000 – Rp 400.000
= Rp 600.000
Pajak penghasilan 10 %
Ditanya: gaji yang diterima ibu tersebut
Jawab:
Besar pajak penghasilan = 10 % x Rp 600.000
= x Rp 600.000
= Rp 60.000
Jadi besar gaji yang diterima ibu tersebut adalah
= Rp 1.000.000 – Rp 60.000
= Rp 940.000
LATIHAN
1. Seorang pedagang membeli telur 10 kg dengan harga Rp 120.000, kemudian telur itu dijual denan harga Rp12.500/kg. Berapakah keuntungan pedagang tersebut?
2. Dari soal no.1 jika dari 10 kg telur pecah 1 kg sehingga tidak dapat dijual, maka berapakah persentase kerugian yang ditanggung pedagang?
3. Dalam sebuah toko terdapat diskonan, baju dengan harga Rp 40.000 didiskon 10 %, celana seharga Rp 70.000 didiskon 15 %, topi seharga 20.000 didiskon 5 %, tas seharga 35.000 didiskon 5 %, dan kaos seharga Rp 55.000 didiskon 25 %. Jika Yuda ingin berbelanja dengan menghabiskan uang antara Rp 130.000 s/d Rp 150.000 maka barang apa saja yang akan Yuda beli?
4. Ahmad membeli sepeda motor dengan harga Rp 15.000.000 dengan pajaknya 10 %, setelah beberapa tahun Ahmad menjual mator tersebut dengan harga Rp 11.500.000. berapakah kerugian yang diderita Ahmad?
Penyelesaian:
1. Diketahui: harga beli 10 kg telur Rp 120.000
   Harga jual 1 kg telur Rp 12.500
   Ditanya: keuntungan pedagang?
   Jawab:
   Untung = Harga Jual – Harga Beli
   Harga jual = 10 x Rp 12.500
   = Rp 125.000
   Untung = Rp 125.000 – Rp 120.000
   = Rp 5.000
    Jadi pedagang itu mendapat keuntungan Rp 5000
2. Diketahui: Harga beli 10 kg telur Rp 120.000
   Harga jual 1 kg telur Rp 12.500
   Telur yang dapat dijual 10 kg – 1 kg = 9 kg
   Ditanya: Persentase kerugian yang ditanggung pedagang?
   Jawab:
   Persentase Rugi = x 100 %
   Rugi = harga beli – harga jual
   Harga jual = 9 x Rp 12.500
                     = Rp 112.500
   Rugi = Rp 120.000 – Rp 112.500
            = Rp 7.500
   Persentase Rugi = 6,25 %
  Jadi persentase kerugiannya adalah 6,25 %.
3. diketahui: Harga baju Rp 40.000, diskon 10 %
    Harga celana Rp 70.000, diskon 15 %
    Harga topi Rp 20.000, diskon 5 %
    Harga tas Rp 35.000,diskon 5 %
    Harga kaos Rp 55.000,diskon 15 %
    Uang belanja Rp 130.000 s/d Rp 150.000
    Ditanya: Barang apa saja yang bisa dibeli Yuda?
    Jawab:
Harga setelah didiskon:
    Baju = 40.000 – (10 % x Rp 40.000) = 40.000 – 4000 = 36.000
    Celana = 70.000 – (15% x Rp 70.000) = Rp 64.500
    Topi = 20.000 – (5 % x Rp 20.000) = Rp 19.000
    Tas = Rp 35.000 – ( 5 % x Rp 35.000) = Rp 33.250
    Kaos = Rp 55.000 – (15 % x Rp 55.000) = Rp 41.250
Jadi barang yang dapat dibeli Yuda adalah

• Celana, tas, kaos 
• Baju, celana, tas 
• Baju, celana, kaos

4. Diketahui: harga beli Rp 15.000.000
    Pajak 10 % = 10 % x 15.000.000 = Rp 500.000
    Harga jual Rp 11.500.000
    Ditanya: kerugian?
    Jawab:
    Besar modal ( harga beli + pajak) = Rp 15.000.000 + Rp 500.000
                                                          = Rp 15.500.000
    Rugi = Rp 15.500.000 – Rp 11.500.000
            = Rp 4.000.000
Jadi kerugian yang diderita Ahmad adalah Rp 4.000.000.